Q.
India's Mangalyan was sent to the Mars by launching it into a transfer orbit $EOM$ around the sun. It leaves the earth at $E$ and meets Mars at $M$. If the semi-major axis of Earth's orbit is $a_e$ = $1.5 \times 10^{11} m$, that of Mar's orbit $a_m = 2.28 \times 10^{11} m$, taken Kepler's laws give the estimate of time for Mangalyan to reach Mars from Earth to be close to :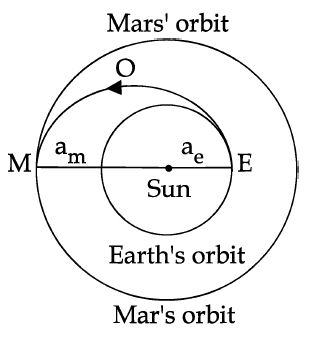
Solution: