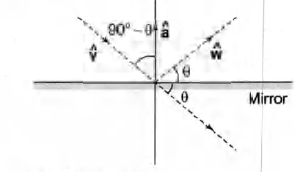
Question

Incident ray is along the unit vector $\hat{ v }$ and the reflected ray is along the unit vector $\hat{ w }$. The normal is along unit vector $\hat{ a }$ outwards. Express $\hat{ w }$ in terms of $\hat{ a }$ and $\hat{ v }$.

Answer 1

Since, $\hat{ v }$ is unit vector along the incident ray and $\hat{ w }$ is the unit vector along the reflected ray.
Hence, $\hat{a}$ is a unit vector along the external bisector of $\hat{ v }$ and $\hat{ w }_{i}$
$\therefore \hat{ w }-\hat{ v }=\lambda \hat{ a }$

On squaring both sides, we get
$\Rightarrow 1+1-\hat{ w } \cdot \hat{ v }=\lambda^{2} \Rightarrow 2-2 \cos 2 \theta=\lambda^{2} $
$\Rightarrow \lambda=2 \sin \theta$
where, $2 \theta$ is the angle between $\hat{ v }$ and $\hat{ w }$.
Hence, $ \hat{ w }-\hat{ v }=2 \sin \theta \cdot \hat{ a }=2 \cos \left(90^{\circ}-\theta\right) \hat{ a }=-(2 \hat{ a } \cdot \hat{ v }) \hat{ a }$
$\Rightarrow \hat{ w }=\hat{ v }-2(\hat{ a } \cdot \hat{ v }) \hat{ a }$