Q.
In Young's double slit experiment, two slits $S_1$ and $S_2$ are ' $d$ ' distance apart and the separation from slits to screen is $D$ (as shown in figure). Now if two transparent slabs of equal thickness $0.1 \,mm$ but refractive index $1.51$ and $1.55$ are introduced in the path of beam $(\lambda=4000 \mathring {A})$ from $S_1$ and $S_2$ respectively, The central bright fringe spot will shift by ______number of fringes.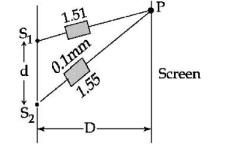
Solution:
