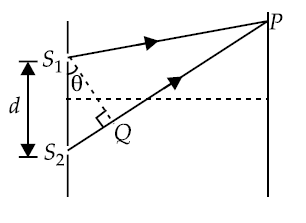
Q. In Young’s double slit experiment, intensity at a point is $\left(\frac{1}{4}\right)$ of the maximum intensity. Angular position of this point is
Wave Optics
Solution:
In Young’s double slit experiment, intensity at any point $P$ is given by
$I=I_{max}\,cos^{2}\left(\frac{\phi}{2}\right)$
where $\phi$ is the phase difference
According to question, $I=\frac{I_{max}}{4}$
$\frac{I_{max}}{4}=I_{max}\,cos^{2}\left(\frac{\phi }{2}\right)$ or $cos\frac{\phi }{2}=\frac{1}{2}=cos \frac{\pi}{3}$
$\therefore \phi=\frac{2\pi}{3}$
If $Δx$ is the path difference between two waves, then
$\frac{\phi}{2\pi}=\frac{\Delta x}{\lambda}$
or $\Delta x=\frac{\lambda}{2\pi}\phi=\frac{\lambda}{2\pi}\times\frac{2\pi}{3}=\frac{\lambda}{3}$
Phase difference, $Δx = dsin\theta$
or $d\,sin\,\theta=\frac{\lambda}{3}$ or $\theta=sin^{-1}\left(\frac{\lambda}{3d}\right)$