Question

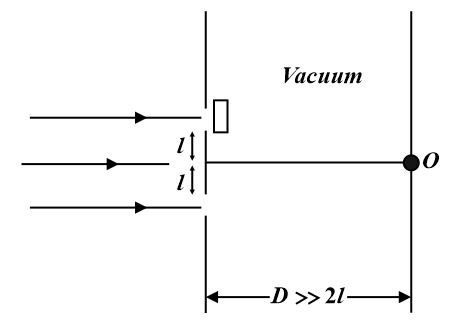
In Young's double-slit experiment, both the slits produce equal intensities on a screen. A $100\%$ transparent thin film of refractive index $\mu =1.5$ is kept in front of one of the slits, due to which the intensity at the point $O$ on the screen becomes $75\%$ of its initial value. If the wavelength of monochromatic light is $720 \, nm$ , then what is the minimum thickness (in $nm$ ) of the film?

Answer 1

The path difference at the point $O$ is
$\Delta x =(\mu-1) t $
$ I =4 l _0 \cos ^2 \frac{\Phi}{2} $
$0.75(4 I _0)=4 I _0 \cos ^2 \frac{\Phi}{2} $
$\Rightarrow \cos \frac{\Phi}{2}=\pm \frac{\sqrt{3}}{2}$
$\Rightarrow \Phi_{\min }=60^{\circ} $
$\Phi_{\min }=\frac{2 \pi}{\lambda} \Delta x =\frac{2 \pi}{\lambda} \mu-1 t =\frac{\pi}{3} $
$ t =\frac{\lambda}{6 \mu-1}=\frac{\lambda_0}{61.5-1}=240 \,nm$