Question

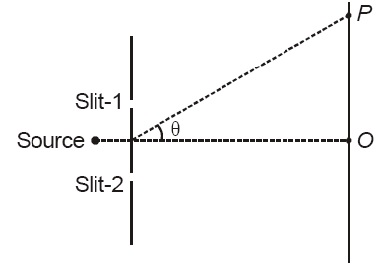
In the YDSE arrangement shown here, the intensity on the screen due to slit-2 is four times that of slit-1. If resultant intensity at the position of central maxima $O$ is $I$ , the resultant intensity at point P, where the phase difference between two waves coming from two slits is $\left(\text{cos}\right)^{-1} \left(\frac{1}{4}\right)$ is

• A. $\frac{I}{3}$
• B. $\frac{2 I}{3}$
• C. $\frac{I}{4}$
• D. $\frac{I}{2}$

Answer 1

Answer: (B)

$I = \left(\sqrt{I_{0}} + \sqrt{4 I_{0}}\right)^{2} = 9 I_{0}$
$I_{\text{0}} \text{=} \frac{I}{\text{g}}$
$I^{'} = I_{0} + 4 I_{0} + 2 \sqrt{I_{0} \text{.} 4 I_{0}} \times \frac{1}{4}$
$= 6 I_{0}$
$= \frac{2}{3} I$