Question

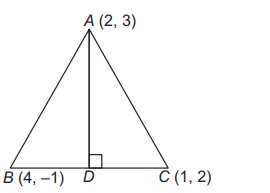
In the $\triangle A B C$ with vertices $A(2,3), B(4,-1)$ and $C(1,2)$
I. The equation of altitude from the vertex $A$ is $x-y+1=0$.
II. The length of altitude from the vertex $A$ is $\sqrt{2}$.

• A. Both I and II are true
• B. Only I is true
• C. Only II is true
• D. Both I and II are false

Answer 1

Answer: (A)

Given, vertices of a $\triangle A B C$ are $A(2,3), B(4,-1)$ and $C(1,2)$.
$ \because $ Line $A D \perp $ Line $ B C$
$ \therefore $ Slope of $ A D \times $ Slope of $ B C=-1 $
$ \Rightarrow m \times \frac{y_2-y_1}{x_2-x_1}=-1 $
$ \Rightarrow m \times \frac{2+1}{1-4}=-1$
$ \left(\because x_1=4, y_1=-1, x_2=1, y_2=2\right)$
$ \Rightarrow m \times \frac{3}{-3}=-1 \Rightarrow m=1$

Hence, equation of $A D$, by using $y-y_1=m\left(x-x_1\right)$ where $\left(x_1, y_1\right)=(2,3)$ and $m=1$, is
$y-3=1(x-2)$
$\Rightarrow x-y-2+3=0 \Rightarrow x-y+1=0$
Now, equation of $B C$ by using $y-y_1-\frac{y_2-y_1}{x_2-x_1}\left(x-x_1\right)$, is
$ y+1=\frac{2+1}{1-4}(x-4)$
$ \left(\because x_1=4, y_1=-1, x_2=1, y_2=2\right) $
$\Rightarrow y+1=\frac{3}{-3}(x-4)$
$ \Rightarrow y+1=-x+4 \Rightarrow x+y-3=0 $
$\therefore$ Length of $A D=$ Perpendicular distance from $(2,3)$ to the line $B C$
i.e., $x+y-3=0 $
$ =\left|\frac{2+3-3}{\sqrt{1^2+1^2}}\right|=\frac{2}{\sqrt{2}}=\sqrt{2} $
$\left(\because p=\left|\frac{a x_1+b y_1+c}{\sqrt{a^2+b^2}}\right|\right) $