Q.
In the system shown in figure, masses of the blocks are such that when system is released, the acceleration of pulley $P_{1}$ is $a$ upward and acceleration of block $A$ is $a_{1}$ upward. It is found that the acceleration of block $C$ is same as that of $A$ both in magnitude and direction $\left(a_{1} > a > a_{1} / 2\right)$. Then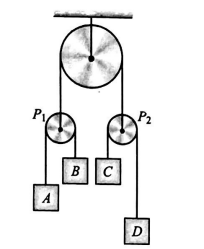
Laws of Motion
Solution: