Q.
In the situation in figure, a block of mass $1\, kg$ is attached to a light spring of constant $40 \,N / m$ whose other end is fixed to the roof of a building $50 \,cm$ above the smooth horizontal surface. Initially, spring is in natural length and vertical. When a force $F=20 \sqrt{3} N$ is applied on the block, the block starts to move. The speed at the instant it breaks off the surface below it is $\sqrt{10 n} \,m / s$. The value of $n$ is________.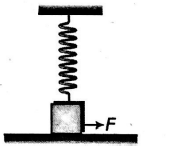
Work, Energy and Power
Solution:
