Q.
In the shown figure, half a period of $\sin x$ from 0 to $\pi$ is split into two regions (light and dark shaded) of equal area by a line through the origin. If the line and the sine function intersect at a point whose $x$ co-ordinate is $k$, then $k$ satisfies the equation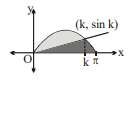
Application of Integrals
Solution: