Q.
In the right angle triangle as shown, an altitude is drawn from the right angle vertex to the hypotenuse. Circles are inscribed within
each of the smaller triangles. What is the distance between the centres of these circles?
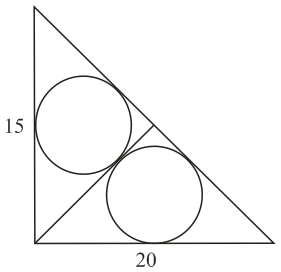
NTA AbhyasNTA Abhyas 2022
Solution:
