Question

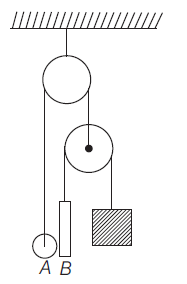
In the pulley system shown n the figure, the mass of $A$ is half of that of $\operatorname{rod} B$. The rod length is $500 \,cm$. The mass of pulleys and the threads may be neglected. The mass $A$ is set at the same level as the lower end of the rod and then released. After releasing the mass $A$, it would reach the top end of the $\operatorname{rod} B$ in time (Assume, $g=10 \,m / s ^{2}$ )

• A. 2.0 s
• B. 1.0 s
• C. 3.0 s
• D. 4.0 s

Answer 1

Answer: (B)

According to the question,

Given, mass of body $A$, is half of mass of $\operatorname{rod} B$.
i.e., $m_{A}=\frac{m_{B}}{2} \Rightarrow m_{B}=2\, m_{A}$
and length of $\operatorname{rod}=500\,cm =5 \,m$
Since, $\operatorname{rod} B$ and body $C$ is in equilibrium, hence mass of $\operatorname{rod} B=$ mass of $\operatorname{rod} C$
i.e., $m_{B}=m_{C}$
By applying Newton's law of motion,
$2 \,T-m_{A} g=m_{A} a \,....(i)$
$\left(m_{B}+m_{C}\right) g-2 T=\left(m_{B}+m_{C}\right) a$
or $2 \,m_{B} g-2 T=2 m_{B} a $
or $4 \,m_{A} g-2 T=4 m_{A} a\,....(ii)$
Adding Eqs. (i) and (ii), we get
$3 \,m_{A} g =5 m_{A} a $
$a =\frac{3}{5} g=\frac{3 \times 10}{5}=6 m / s ^{2}$
If $t$ be the time to cross the rod of length
$500 \,cm =5\,m$
$\therefore $ From Eqs., $s=0+\frac{1}{2} a t^{2}$
$\Rightarrow t=\sqrt{\frac{2 s}{a}}=\sqrt{\frac{2 \times 5}{6}}=1.28 s \approx 1 s$