Q.
In the given network capacitance $C_{2}=10\, \mu F,\, C_{1}=5\, \mu F$ and $C_{3}=4\, \mu F$. The resultant capacitance between $P$ and $Q$ will be :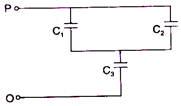
Rajasthan PMTRajasthan PMT 2005Electrostatic Potential and Capacitance
Solution: