Q.
In the given figure, the equation of the larger circle is $x^{2}+y^{2}+4 y-5=0$ and the distance between centres is
$4$ . Then the equation of smaller circle is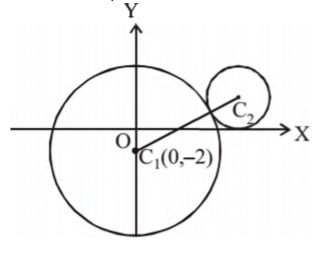
BITSATBITSAT 2020
Solution:

Solution: