Q.
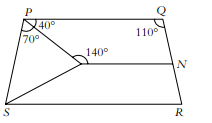
In the given figure, $P Q R S$ is an isosceles trapezium and $\overline{P Q}|| \overline{S R}|| \overline{M N}$. If $\angle S P M=70^{\circ}$ and $\angle P Q R=110^{\circ}$, then find $\angle P M N$.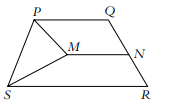
Geometry
Solution:
Given that $P Q R S$ is an isosceles trapezium, $\overline{P Q}|| \overline{S R}|| \overline{M N}$.
$\angle S P M=70^{\circ}$ and $\angle P Q R=110^{\circ}$ (given)
$\Rightarrow \angle P Q R=\angle S P Q=110^{\circ}$
$\angle M P Q=\angle S P Q-\angle S P M=110^{\circ}-70^{\circ}$ $=40^{\circ}$
$\overline{P Q}|| \overline{M N} \Rightarrow \angle P M N=180^{\circ}-\angle M P Q$
$=180^{\circ}-40^{\circ}=140^{\circ}$