Q.
These are numeric entry type questions.
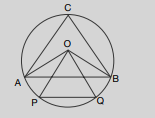
In the given figure, ' $O ^{\prime}$ is the centre of the circle. $\triangle ABC$ and $\triangle OPQ$ are equilateral triangles. $\overline{ AB }$ is parallel to $\overline{ PQ }$. Then $\angle OQA +$ $\angle ACQ =$______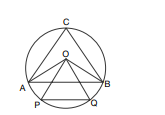
Geometry
Solution: