Question

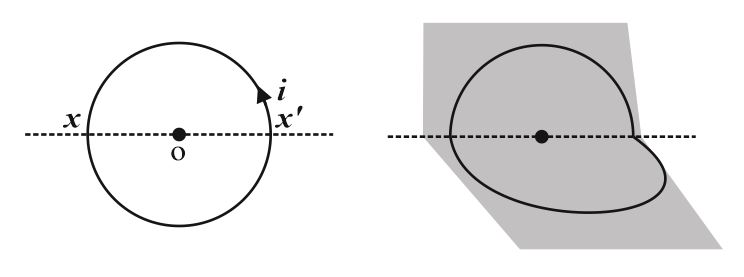
In the given figure magnetic field at the centre of ring $O$ is $\frac{8}{\sqrt{2}} T$. Now it is turned through $90^{\circ}$ about $x x^{\prime}$ axis, so that two semicircular parts are mutually perpendicular. What is the new value of the magnetic field (in $T$ ) at the centre?

Answer 1

Magnetic field at the centre of the circular ring is $\frac{8}{\sqrt{2}} \quad$ T. Therefore, magnetic field due to a semicircular ring will be $\frac{1}{2} \times \frac{8}{\sqrt{2}}=\frac{4}{\sqrt{2}} \quad T$.
When the ring is bent as given in the question, the magnetic fields due to the semicircular part will also be perpendicular to each other. Hence, the net magnetic field will be.
$B=\sqrt{\frac{4}{\sqrt{2}}^{2}+\frac{4}{\sqrt{2}}^{2}}=4 T$