Q.
In the given figure, $C$ is middle point of lines $S_{1}\, S_{2} .$ A monochromatic light of wavelength $\lambda$ is incident on slits. The ratio of intensities of $S_{3}$ and $S_{4}$ is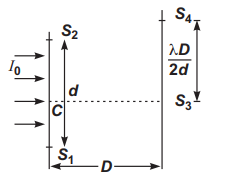
Wave Optics
Solution: