Q.
These are numeric entry type questions.
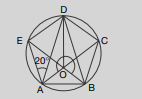
In the given figure, $ABCDE$ is a pentagon, inscribed in a circle with centre ${ }^{\prime} O ^{\prime}, CD = DE$ and $AD = BD , \angle EAD =20^{\circ}$ and $\angle BOC =100^{\circ}$. Then, $\angle DAO +\angle BAO =$____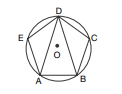
Geometry
Solution: