Q.
In the given circuit, the reading of voltmeters $V_{1}$ and $V_{2}$ are 300 volt each. The reading of the voltmeter $V_{3}$ and ammeter $A$ are, respectively.
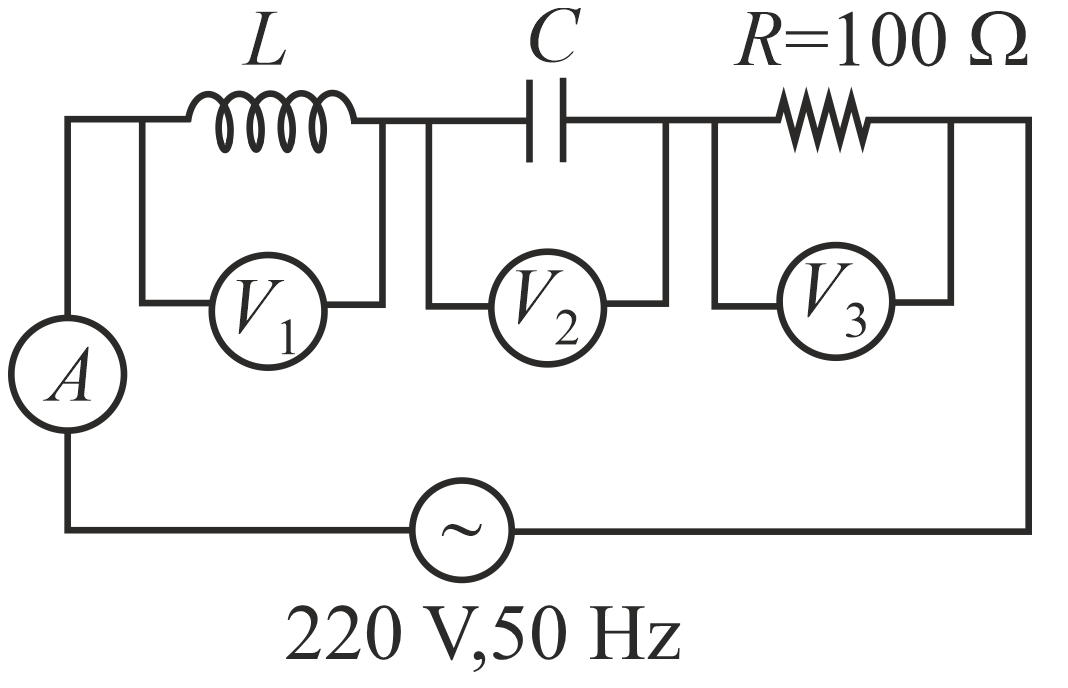
NTA AbhyasNTA Abhyas 2022
Solution:
Total potential difference across a series LCR circuit is given by, $V=\sqrt{V_{R}^{2} + \left(\right. V_{L} - V_{C} \left.\right)^{2}}...\left(1\right)$
where, $V_{R}\text{,}V_{L}\text{ and }V_{C}$ are the potential drop across resistor, inductor and capacitor, respectively.
$V_{L}=V_{C}$ because $V_{1} = V_{2}$
Hence, equation $\left(1\right)$ becomes $V=V_{R}=220V$
Now, using Ohm's law,
Current, $I = \frac{V}{R} = \frac{220}{100} = 2.2 A$
Hence, reading of voltmeter $V_{3}$ and ammeter $A$ are $220V\text{ and}2.2A$ , respectively.
where, $V_{R}\text{,}V_{L}\text{ and }V_{C}$ are the potential drop across resistor, inductor and capacitor, respectively.
$V_{L}=V_{C}$ because $V_{1} = V_{2}$
Hence, equation $\left(1\right)$ becomes $V=V_{R}=220V$
Now, using Ohm's law,
Current, $I = \frac{V}{R} = \frac{220}{100} = 2.2 A$
Hence, reading of voltmeter $V_{3}$ and ammeter $A$ are $220V\text{ and}2.2A$ , respectively.