Q.
In the following figure the masses of the blocks $A$ and $B$ are same and each equal to $m$. The tensions in the strings $O A$ and $A B$ are $T_{2}$ and $T_{1}$, respectively. The system is in equilibrium with a constant horizontal force mg on $B$. Then $T_{1}$ is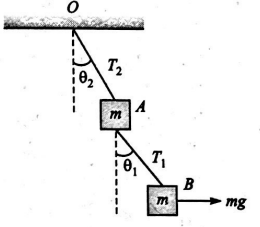
Laws of Motion
Solution:
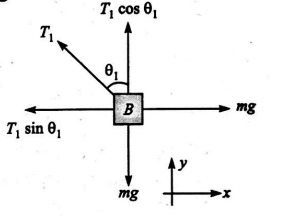
Considering free body diagram of block $B$
$\Sigma F_{x}=0 ; T_{1} \cos \theta_{1}=m g$ ...(i)
$\Sigma F_{y}=0 ; T_{1} \cos \theta_{1}=-m g$ ...(ii)
By squaring and adding equations
(i) & (ii), we get
$T_{1}^{2}\left(\sin ^{2} \theta_{1}+\cos ^{2} \theta_{1}\right)=2(m g)^{2}$
$\therefore T_{1}=\sqrt{2} m g$