Q.
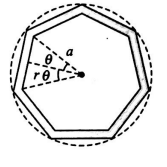
In the following figure a wire bent in the form of a regular polygon of $n$ sides is inscribed in a circle of radius $a$. Net magnetic field at centre will be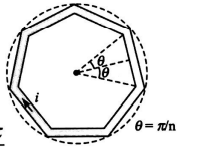
Moving Charges and Magnetism
Solution:
Magnetic field at the centre due to one side
$B_{1}=\frac{\mu_{0}}{4 \pi} \cdot \frac{2 i \sin \theta}{r}$
where $r=a \cos \theta$
So $B_{1}=\frac{\mu_{0}}{4 \pi} \cdot \frac{2 i \sin \theta}{a \cos \theta}=\frac{\mu_{0} i}{2 \pi a} \tan \theta$
Hence net magnetic field
$B_{\text {net }}=n \times \frac{\mu_{0} i}{2 \pi a} \tan \frac{\pi}{n}$