Question

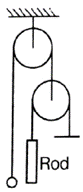
In the figure, the mass of a ball is $\frac{9}{5}$ times the mass of the rod. Length of the rod is $1 \, m$ . The level of ball is the same as rod level. Find out the time taken by the ball to reach at the upper end of the rod.

• A. $1.4 \, s$
• B. $2.45 \, s$
• C. $3.25 \, s$
• D. $5 \, s$

Answer 1

Answer: (A)

Let $a_{1} \, $ and $ \, a_{2}$ be accelerations of a ball (upward) and rod (downward), respectively.

Clearly, from the diagram
$2a_{1}-a_{2}$ ...(i)
Now, for the ball
$2T-\frac{9}{5}mg-\frac{9}{5}ma$ ...(ii)
and for the rod, $mg-T=ma_{2}$ ...(iii)
On solving equations (i) and (iii), we get
$a_{1}=\frac{g}{29} \, ms^{- 2}\uparrow$ (upward)
$a_{2}=\frac{2 g}{29} \, ms^{- 2}\downarrow$ (downward)
So, acceleration of ball w.r.t rod $=a_{1}+a_{2}=\frac{3 g}{29}$
Now, displacement of ball w.r.t. rod when it reaches the upper end of rod is $1m$ .
Using the equation of motion,
$s=ut+\frac{1}{2}at^{2}$
$s=0+\frac{1}{2}\times \frac{3 \times 10}{29}t^{2}$
$t=\sqrt{\frac{58}{30}}=1.4 \, s \, \left(a p p r o x\right)$