Q.
In the figure, the ball $A$ is released from rest when the spring is at its natural length. For the block $B$ of mass $M$ to leave contact with the ground at same stage, the minimum mass of $A$ must be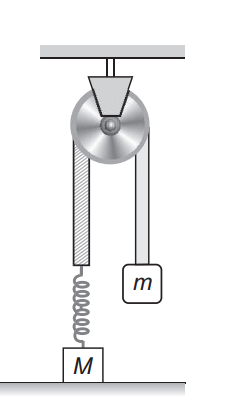
Laws of Motion
Solution:
