Question

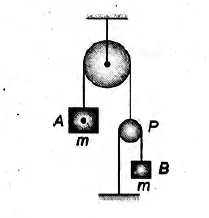
In the figure shown, the system is released from rest. Find the velocity of blocks when block B has fallen a distance $l$. Assume all pulleys to be massless and frictionless

• A. $v=\sqrt{\frac{2gl}{5}} $
• B. $v=\sqrt{\frac{gl}{5}}$
• C. $v=\sqrt{\frac{gl}{3}}$
• D. None of these

Answer 1

Answer: (B)

Evidently, when the block $B$ descends by a distance l.
The pulley $P$, descends by a distance $\frac{l}{2}$, and
consequently, the block $A$ ascends by a distance $\frac{l}{2}$.
Also, if $v$ be the speed of block $A,(u p), 2 v$, would be the speed of block $B$ (down).
Net loss in P.E. of the system
$=$ Loss in P.E of block $B -$ gain in P.E. of block $A$
$=m g l-m g \frac{l}{2}=m g \frac{l}{2}$
Total gain in K.E. = $\frac{1}{2} m v^{2}+\frac{1}{2} m(2 v)^{2}$
$=\frac{5}{2} m v^{2}$
Now, law of conservation of energy demands
Loss in P.E. = Gain in K.E.
$m g \frac{l}{2}=\frac{5}{2} m v^{2}$
$\Rightarrow v^{2}=\frac{g l}{5}$
$v=\sqrt{\frac{g l}{5}}$