Q.
In the figure given below, for an angle of incidence $45^\circ $ at the top surface, what is the minimum refractive index needed for total internal reflection at the vertical face?
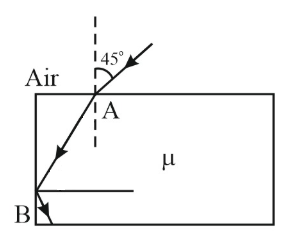
NTA AbhyasNTA Abhyas 2020Ray Optics and Optical Instruments
Solution:
