Question

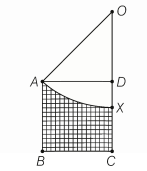
In the figure, $ABCD$ is a unit square. $A$ circle is drawn with centre $O$ on the extended line $CD$ and passing through $A$. If the diagonal $AC$ is tangent to the circle, then the area of the shaded region is

• A. $\frac{9-\pi}{6}$
• B. $\frac{8-\pi}{6}$
• C. $\frac{7-\pi}{4}$
• D. $\frac{6-\pi}{4}$

Answer 1

Answer: (D)

Given, $ABCD$ is a square
$AB = CD = AD = BC = 1$
$AC$ is tangent of circle
$\angle OAC = 90^{\circ}$
$\angle CAD = 45^{\circ}$
$\therefore \angle OAD = 45^{\circ}$
$\therefore OA = \sqrt{2}$

$\therefore$ Area of shaded region
$=$Area of square $+$ Area of $\Delta AOD -$ Area of sector
$= 1 + \frac{1}{2} \times 1 - \frac{45}{360} \times (\sqrt{2})^2 \cdot \pi$
$= 1 + \frac{1}{2} - \frac{\pi}{4} = \frac{3}{2} - \frac{\pi}{4} = \frac{6 - \pi}{4}$