Q.
In the figure, a ladder of mass $m$ is shown leaning against a wall. It is in static equilibrium making an angle $\theta$ with the horizontal floor. The coefficient of friction between the wall and the ladder is $\mu_{1}$ and that between the floor and the ladder is $\mu_{2}$. The normal reaction of the wall on the ladder is $N _{1}$ and that of the floor is $N _{2}$. If the ladder is about to slip, then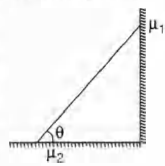
Solution: