Question

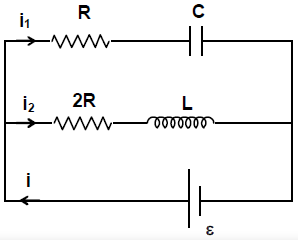
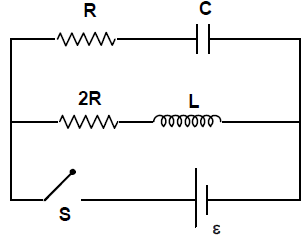
In the circuit shown in the figure switch $S$ is closed at $t=0$ . Then which of the following statements is WRONG.
$\left(Given : R = \sqrt{\frac{L}{2 C}}\right)$

• A. Initial current through the battery is $\epsilon /R$ .
• B. After a long time current through battery is $\frac{\epsilon }{2 R}$ .
• C. The current in the battery is $\frac{5}{8}$ times its initial value at $t=RCln2$ .
• D. The currents in the inductor and the capacitors are equal at $t=RCln3$ .

Answer 1

Answer: (C)

since $RC=\frac{L}{2 R}$
$\Rightarrow $ time constants for both branches are equal.
$i_{1}=\frac{\epsilon }{R}e^{- t / R C}$
$i_{2}=\frac{\epsilon }{2 R}\left(1 - e^{- t / R C}\right)$
$i=i_{1}+i_{2}=\frac{\epsilon }{2 R}+\frac{\epsilon }{2 R}e^{- t / R C}$
$i_{max}=\frac{\epsilon }{R}$
When, $i=\frac{5 \epsilon }{8 R}=\frac{\epsilon }{2 R}+\frac{\epsilon }{2 R}e^{- t / R C}$
$\Rightarrow t=RCln4=2RCln2$
$i_{1}=i_{2}$
$\Rightarrow \frac{\epsilon }{R}e^{- t / R C}=\frac{\epsilon }{2 R}\left(1 - e^{- t / R C}\right)$
$\Rightarrow t=RCln3$