Q.
In the circuit shown in figure, the battery is an ideal one, with
emf $V$. The capacitor is initially uncharged. The switch $S$ is
closed at time $t = 0$.
(a) Find the charge $Q$ on the capacitor at time $t$.
(b) Find the current in $AB$ at time $t$. What is its limiting value
as $t \rightarrow \infty ? $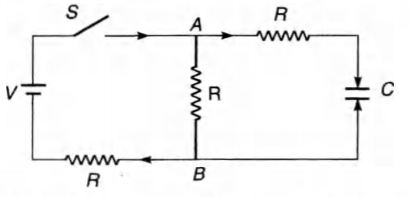
IIT JEEIIT JEE 1998Electrostatic Potential and Capacitance
Solution:
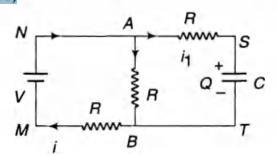
Let at any time I charge on capacitor C be Q and currents are
as shown. Since, charge Q will increase with time t.
Therefore,
$i_1= \frac {dQ}{dt} $
(a) Applying Kirchhoff's second law in loop MNABM
$V=(i-i_1)R+iR $
or $\, \, \, \, \, \, \, \, V=2iR-i_1R \, \, \, \, \, \, \, \, \, \, ...(i) $
Similarly, applying Kirchhoff's second law in loop
MNSTM, we have
$V=i_1R+ \frac {Q}{C}+iR \, \, \, \, \, \, \, \, \, ...(ii) $
Eliminating i from Eqs. (i) and (ii), we get
$V=3i_1R+ \frac {2Q}{C} $
or $\, \, \, \, \, 3i_1R=V- \frac {2Q}{C} $
or $\, \, \, \, \, i_1= \frac {1}{3R}\bigg (V- \frac {2Q}{C}\bigg ) $
or $ \, \, \, \, \, \frac {dQ}{dt}= \frac {1}{3R}\bigg (V- \frac {2Q}{C}\bigg ) $
or $ \, \, \, \, \, \frac {dQ}{V- \frac {2Q}{C}}= \frac {dt}{3R} $
or $\int _0^Q \frac {dQ}{V- \frac {2Q}{C}}= \int _0^t \frac {dt}{3R} $
This equation gives
$\, \, \, \, \, \, Q= \frac {CV}{2}(1-e^{-2t/3RC}) $
(b) $\, \, \, \, \, \, i_1= \frac {dQ}{dt}= \frac {V}{3R}e^{-2t/3RC} $
From Eq. (i)
$i= \frac {V+i_1R}{2R}= \frac {V+ \frac {V}{3}e^{-2t/3RC}}{2R} $
$\therefore $ Current through AB
$i_2=i-i_1= \frac {V+ \frac {V}{3}e^{-2t/3RC}}{2R}- \frac {V}{3R}e^{-2t/3RC} $
$i_2= \frac {V}{2R}- \frac {V}{6R}e^{-2t/3RC} $
$i_2= \frac {V}{2R} as \, t \rightarrow \infty $