Question

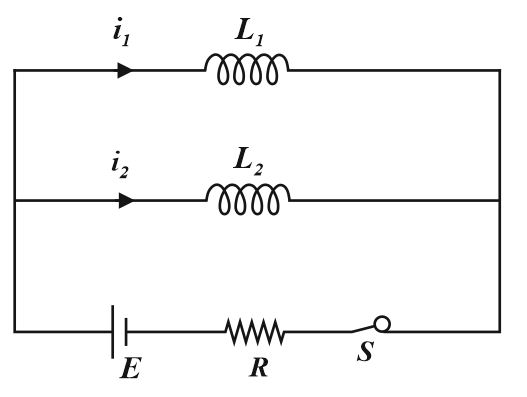
In the circuit shown below, $i_{1}$ and $i_{2}$ are the steady-state values of the current through $L_{1}$ and $L_{2}$ respectively, then $i_{1}$ is

• A. $i_{1 =}\frac{E L_{2}}{R \left(L_{1} + L_{2}\right)}$
• B. $i_{1 =}\frac{E L_{1}}{R \left(L_{1} + L_{2}\right)}$
• C. $i_{1 =}\frac{E L_{2}}{R \sqrt{L_{1} L_{2}}}$
• D. $i_{1 =}\frac{E L_{1}}{R \sqrt{L_{1} L_{2}}}$

Answer 1

Answer: (A)

Since the potential difference across the inductors is same, we get
$L_{1}\frac{d i_{1}}{d t}=L_{2}\frac{d i_{2}}{d t}$
$L_{1}di_{1}=L_{2}di_{2}$
$L_{1}\Delta i_{1}=L_{2}\Delta i_{2}$
$L_{1}i_{1}=L_{2}i_{2}$ (Since the initial value of current through both the inductors was zero)
$\frac{i_{1}}{i_{2}}=\frac{L_{2}}{L_{1}}$
The steady current $i$ passing through $R$ is
$\textit{i}=\frac{\textit{E}}{\textit{R}}$
$i_{1}=\left(\frac{L_{2}}{L_{1} + L_{2}}\right)i=\frac{E L_{2}}{R \left(L_{1} + L_{2}\right)}$