Q.
In the circuit of figure, the battery emf is $50 V$, the resistance is $200 \Omega$, and the capacitance is $1.0 \mu F$. The switch $S$ is closed for a long time interval, and zero potential difference is measured across the capacitor.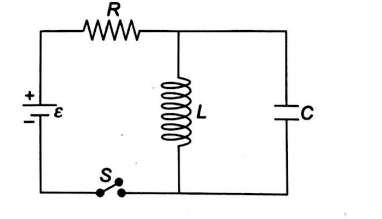
Alternating Current
Solution: