Question

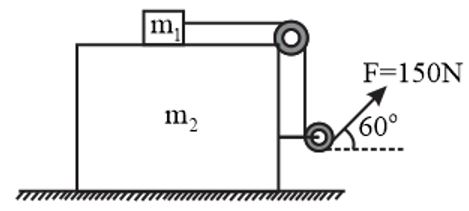
In the arrangement shown in the figure, friction exists only between the two blocks, $A$ and $B$ . The coefficient of static friction $\mu _{s}=0.6$ and coefficient of kinetic friction $\mu _{k}=0.4$ , the masses of the blocks $A$ and $B$ are $m_{1}=20 \, kg$ and $m_{2}=30 \, kg$ , respectively. Find the acceleration (in $m \, s^{- 2}$ ) of $m_{1}$ , if a force $F=150 \, N$ is applied, as shown in the figure. [Assume that string and pulleys are massless]

Answer 1

Let us assume that the two blocks move together, without slipping, relative to each other. The acceleration of the system in that case is
$a=\frac{F cos 60 ^\circ }{m_{1} + m_{2}}$
$a=\frac{150 \times 1/2}{20 + 30}=1.5 \, m \, s^{- 2}$
In this case, if the frictional force acting between the two blocks is $f$ , then writing the Newton's second law of motion, for the block of mass $m_{1,}$ we get
$T-f=m_{1}a$
$150-f=20\times 1.5=30$
$f=120 \, N$
$f_{max}=0.6\times 200=120 \, N$
Since $f\leq f_{max}$ , our assumption about the two blocks moving together is correct and hence the acceleration of the blocks is $1.5 \, m \, s^{- 2}$