Question

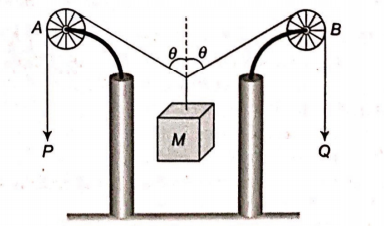
In the arrangement shown in figure the ends $P$ and $Q$ of an non-stretchable string move downwards with uniform speed $U$ Pulleys $A$ and $B$ are fixed. Mass $M$ moves upwards with a speed

• A. $2U\,cos\,\theta$
• B. $U\,cos\,\theta$
• C. $\frac{2U}{cos\,\theta}$
• D. $\frac{U}{cos\,\theta}$

Answer 1

Answer: (D)

As $P$ and $Q$ fall down, the length $l$ decreases at the rate of U m/s
From the figure, $l^{2}=b^{2}+v^{2}$
Differentiating with respect to time
$2l\times \frac{dl}{dt}=2b \times \frac{db}{dt}+2y\times \frac{dy}{dt}$
(As $\frac{db}{dt}=0, \frac{dl}{dt}=U)$
$\Rightarrow \frac{dy}{dt}=\left(\frac{l}{y}\right)\times \frac{dl}{dt}$
$\Rightarrow \frac{dy}{dt}= \left(\frac{1}{cos\,\theta}\right)\times U$
$=\frac{U}{cos\,\theta}$