Question

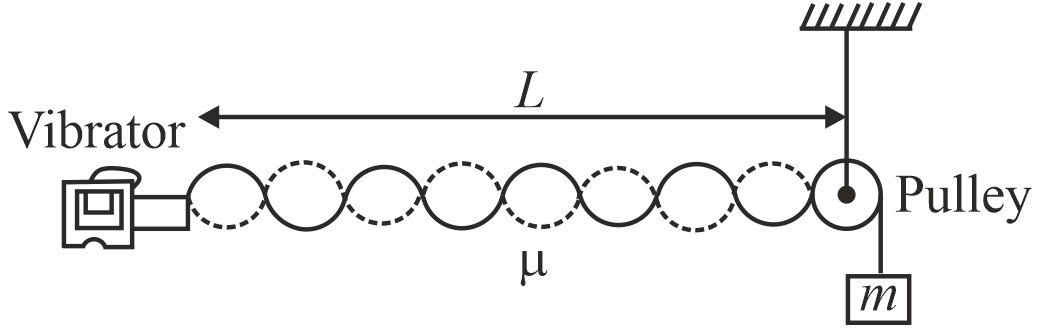
In the arrangement shown in figure, a mass can be hung from a string (with linear mass density of $\mu =0.002\, kg\, m^{- 1}$ ) that passes over a light pulley. The string is connected to a vibrator (of constant frequency $f$ ), and the length of the string between point $P$ and the pulley is $L=2.00\, m$ . When the mass is either $9.0\, kg$ or $25.0\, kg$ , standing waves are observed. $\left(g = 9 . 8\, m s^{- 2}\right).$ What is the frequency (in $Hz$ ) of the vibrator to the nearest integer?

Answer 1

$f=\frac{P}{2 L}\sqrt{\frac{m g}{\mu }}.........\left(i\right)$
$P\sqrt{9}=\left(P - 1\right)\sqrt{25}........\left(ii\right)$
$\therefore P=2.5$
$\therefore \, P\sqrt{9}=\left(P - 2\right)\sqrt{25}$
$\therefore P=5$
$\therefore \, f=\frac{5}{2 \times 2}\sqrt{\frac{88 . 2}{0 .002}}=262.5 \approx 263\, Hz$