Q.
In the above figure, $D E F$ is a triangle whose side $D F$ is produced to $G . H F$ and $H D$ are the bisectors of $\angle E F G$ and $\angle E D G$, respectively. If $\angle D E F=23 \frac{1}{2}^{\circ}$, then $\angle D H F$ (in degrees) $=$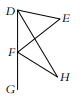
Geometry
Solution: