Question

In the above circuit, $C = \frac{\sqrt{3}}{2} \mu F. \, R_2 \, = \, 20 \Omega, \, L = \frac{\sqrt{3}}{10} \, \, H$ and $R_1 \, = \, 10 \Omega$ Current in $L- R_1$, path is $I_1$ and in C-R$_2$path it is $I_2$ The voltage of A.C source is given by $V = 200 \sqrt{2}$ sin (100t) volts. the phase difference between $I_1$ and $I_2$is :

• A. $30^{\circ}$
• B. $0^{\circ}$
• C. $90^{\circ}$
• D. $60^{\circ}$

Answer 1

Answer: (C)

$x_e \, = \, \frac{1}{\omega} \, = \frac{4}{10^{-6} \, \times \, \sqrt{3} \times 100} \, =\frac{2 \times 10^4}{\sqrt{3}}$
$tan\theta/2 \, \, \frac{x_e}{R_e} \, = \frac{10^3}{\sqrt{3}}$
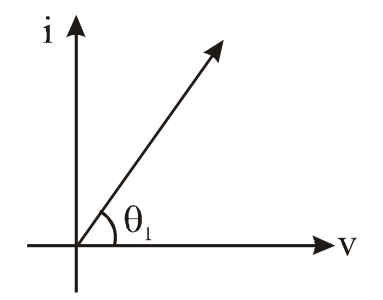
$\theta_1$is close to $90$
For L-R circuit
$x_L \, = \, w_L \, = \, 100 \times \, \frac{\sqrt{3}}{10} \, = \, \sqrt{3}$
tan$\theta_2 \, \, = \, \frac{x_e}{R}$
tan$\theta_2 \, \, = \, \sqrt{3}$
$\theta_2 \, = \, 60$
So phase difference comes out $90 + 60 = 150$.
Therefore Ans. is Bonus
If $R_2$ is 20 K$\Omega$
then phase difference comes out to be $60+30$
= $90^\circ$