Q.
In radius of a circle which is inscribed in a isosceles
triangle one of whose angle is $ 2 \pi / 3, \, is \, \sqrt 3 $, then area
of triangle (in sq units) is
IIT JEEIIT JEE 2006
Solution:
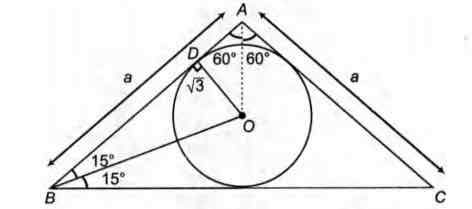
Let AB = AC = a and $ \angle 120^\circ$.
$\therefore $ Area of triangle = $ \frac{1}{2} a^2 \, sin \, 120^\circ $
where, a = AD + BD = $ \sqrt 3 \, tan \, 30^\circ + \sqrt 3 \, cot \, 15^\circ$
$$ = 1 + $ \frac{ \sqrt 3}{ tan \, (45^\circ - 15^\circ)}$
$\Rightarrow a = 1 + \sqrt 3 \bigg( \frac{1 + tan \, 45^\circ \, tan \, 30^\circ}{ tan \, 45^\circ - tan \, 30^\circ}\bigg)$
= 1 + $ \sqrt 3 \bigg( \frac{ \sqrt 3 + 1}{ \sqrt 3 + 1} \bigg) = 4 + 2 \sqrt 3 $
$\therefore $ Area of triangle = $ \frac{1}{2} (4 + 2 \sqrt 3)^2 \bigg( \frac{ \sqrt 3}{2}\bigg) = (12 + 7 \sqrt 3) $ sq units.