Q.
In moving from $A$ to $B$ along an electric field line, the electric field does $6.4 \times 10^{-19} J$ of work on an electron. If $\phi_{1}, \phi_{2}$ are equipotential surfaces, then the potential difference $\left(V_{C}-V_{A}\right)$ is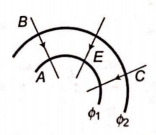
Electrostatic Potential and Capacitance
Solution: