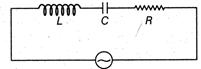
Q. In $ L-C-R $ circuit, $ f=\frac{50}{\pi }Hz, $ $ V=50V, $ If $ L=1H $ and $ C=20\mu C $ , then the voltage across capacitor is
Bihar CECEBihar CECE 2015Alternating Current
Solution:
For an L-C-R circuit, the impedance (Z) is given by
$ \because $ $ Z=\sqrt{{{R}^{2}}+{{({{X}_{L}}-{{X}_{C}})}^{2}}} $ Where $ {{X}_{L}}=\omega L=2\pi {{f}_{1}} $ and $ {{X}_{C}}=\frac{1}{\omega C}=\frac{1}{2\pi fC} $ Given $ f=\frac{50}{\pi }Hz, $ $ R=300\Omega $ and $ L=1H $ and $ C=20\mu C=20\times {{10}^{-6}}C $ $ Z=\sqrt{{{(300)}^{2}}+\left( \frac{^{2\pi \times \frac{50}{\pi }\times 1}1}{2\pi \times \frac{50}{\pi }\times 20\times {{10}^{-6}}} \right)} $ $ Z=\sqrt{90000+{{(100-500)}^{2}}} $ $ \Rightarrow $ $ Z=\sqrt{90000+160000}=\sqrt{250000} $ $ \Rightarrow $ $ Z=500\Omega $ Hence, the current in the circuit is given by $ i=\frac{V}{Z}=\frac{50}{500}=0.1A $ Voltage across capacitor is $ {{V}_{C}}=i{{X}_{C}}=\frac{i}{2\pi fC}=\frac{0.1}{2\pi \times \frac{50}{\pi }\times 20\times {{10}^{-4}}} $ $ =\frac{0.1\times {{10}^{6}}}{100\times 20} $ $ \Rightarrow $ $ {{V}_{C}}=50V $