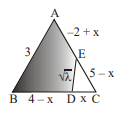Question

In isosceles triangle $ABC$, base $BC =4 cm$ and other sides are measure of $3 cm$. Let $D$ and $E$ points on $BC$ and $AC$ respectively such that $CD + CE =$ semi-perimeter of triangle and area of quadrilateral $BDEA =\frac{1}{2}$ area of triangle $ABC$. If $DE =\sqrt{\lambda}$, then find the value of $\lambda$

Answer 1

$\Delta=\text { area of } \triangle ABC =2 \sqrt{5} $
$CD + CE =5$ .....(i)
$BDEA =\frac{1}{2} \triangle ABC$
$2 \sqrt{5}-\frac{1}{2} x \times(5- x ) \sin C =\frac{1}{2} 2 \sqrt{5}$ .....(ii)
using $\operatorname{cosine~law} \cos C=\frac{2}{3}$
$\therefore \sin C=\frac{\sqrt{5}}{3}$
substituting in (ii) we get
$x =2$ or 3
$x=2 \text { is rejected } $
$\therefore x=3$
$\text { now } \text { using cosine law in } \triangle A B C \text { and EDC } $
$\cos C=\frac{9+16-9}{2 \times 12}=\frac{4+9-\lambda}{12} $
$\lambda=5$