Q.
In given circuit, $C_{1}=C_{2}=C_{3}=C$ initially. Now, a dielectric slab of dielectric constant $K =\frac{3}{2}$ is inserted in $C _{2}$.
The equivalent capacitance become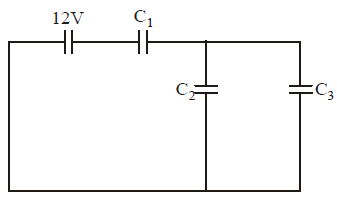
VITEEEVITEEE 2016
Solution:
When a dielectric slab of dielectric constant $K=\frac{3}{2}$ is inserted between the plates of $C_{2}$, its new capacitance $\left(C_{2}'\right)$ becomes
$\left( C _{2}'\right)=\frac{3}{2} C$
Equivalent capacitance of $\left( C _{2}'\right)$ and $C _{3}$ is
$C _{ eq }= C _{2}{ }'+ C _{3}=\frac{3}{2} C + C =\frac{5 C }{2}$
Now, $C _{ eq }$ and $C _{1}$ are in series.
Therefore, their equivalent capacitance is
$C _{ eq }=\frac{ C _{ eq } \times C _{1}}{ C _{ eq }+ C _{1}}=\frac{\frac{5 C }{\frac{2}{5}} \times C }{\frac{5 C }{2}+ C } $
$=\frac{5 C ^{2}}{7 C }=\frac{5 C }{7}$
