Q.
In figure, two blocks are separated by a uniform strut attached to each block with frictionless pins. Block $A$ weighs $400\, N$, block $B$ weighs $300\, N$, and the strut $A B$ weigh $200\, N$. If $\mu=0.25$ under $B$, determine the minimum coefficient of friction under $A$ to prevent motion.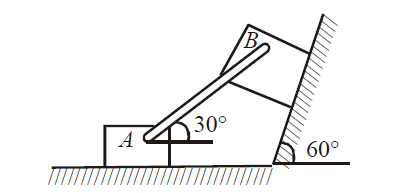
BITSATBITSAT 2015
Solution:
Consider FBD of structure.
Applying equilibrium equations,
$A v+ B v=200\, N$ ...(i)
$A_{H}=B_{H}$ ...(ii)
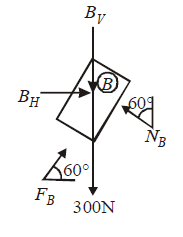
From $FBD$ of block $B$,
$B_{H}+F_{B} \cos 60^{\circ}-N_{B} \sin 60^{\circ}=0$
$N_{B} \cos 60^{\circ}-B_{v}-300+F_{B} \sin 60^{\circ}=0$
$N_{B} \cos 60^{\circ}-B_{v}-300+F_{B} \sin 60^{\circ}=0$
$F_{B}=0.25\, N_{B}=0$
$B_{H}-0.74\, N_{B}=0$ ...(iii)
$-B_{v}+0.71\, N_{B}=300$ ...(iv)
$F_{A}-A_{H}=0$
$N_{A}-A_{V}=400$ ...(v)
$F_{A}=\mu_{A} N_{A}$
$\therefore \mu_{A} N_{A}-A_{H}=0$ ...(iv)
On solving above equations, we get
$N_{A} 650\, N,\,F_{A}=260\, N,\, F_{A}=\mu_{A} N_{A}$
$\therefore \mu_{A}=\frac{260}{250}=0.4$