Q.
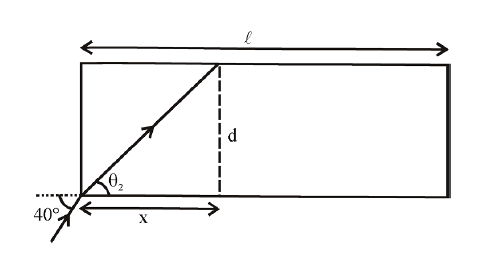
In figure, the optical fiber is $\ell = 2\,m$ long and has a diameter of $d = 20 \,pm$. If a ray of light is incident on one end of the fiber at angle $\theta_1 = 40^{\circ}$, the number of reflection it makes before emerging from the other end is close to: (refractive index o f fibre is $1.31$ and $\sin \; 40^{\circ} = 0.64)$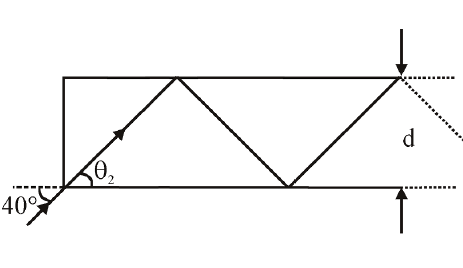
Solution:
Exact solution
by Snells' law $1. \sin40^{\circ} =\left(1.31\right)\sin\theta_{2}$
$ \sin\theta_{2} = \frac{ .64}{1.31} = \frac{64}{131} \approx .49 $
Now $ \tan \theta_{2} = \frac{64}{\sqrt{\left(131\right)^{2} -\left(64\right)^{2}}} = \frac{64}{\sqrt{13065}} \approx \frac{64}{114.3 } =\frac{d}{x} $
Now no. o f reflections
$ = \frac{2\times64}{114.3 \times20\times10^{-6}} = \frac{64 \times10^{5}}{114.3}$
$ \approx55991 \approx 55000 $
Approximate solution
By Snells' law $1.\sin 40^{\circ} = (1.31) \sin \theta_2$
$\sin\theta_{2} = \frac{.64}{1.31} = \frac{64}{131} \approx .49 $
If assume $ \Rightarrow \theta_{2} \approx 30^{\circ} $
$ \tan30^{\circ} = \frac{d}{x} \Rightarrow x = \sqrt{3 } d$
Now number of reflections
$ =\frac{\ell}{\sqrt{3} d} = \frac{2}{\sqrt{3} \times20 \times10^{-6}}= \frac{10^{5}}{\sqrt{3}} $
$ \approx 57735 \approx 57000 $