Q.
In figure given, an electron get accelerated from rest through potential difference $V_{1}=500 \,V$. It enters the gap between two parallel plates having separation $d=20.0\, mm$ and potential difference $V_{2}=100\,V$. The upper plate is at the higher potential. Neglecting fringing and assuming that the electron's velocity vector is perpendicular to the electric field vector between the plates, find the magnitude of uniform magnetic field (in $\times 10^{-3} T$ ) which allows the electron to travel in a straight line in the gap? (Mass of electron $m_{e}=9.0 \times 10^{-31} kg$ )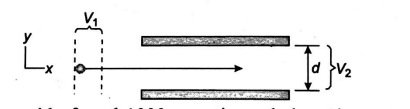
Moving Charges and Magnetism
Solution: