Q.
In figure below, pressure inside a spherical drop is more than pressure outside.
If a liquid drop is in equilibrium, then the pressure difference between the inside and outside of the drop is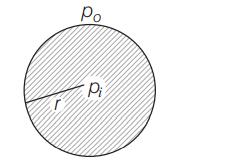
Mechanical Properties of Fluids
Solution: