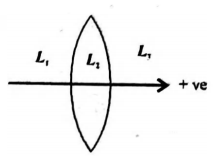
Q.
In Fig. the liquids $L_{1}, L_{2}$ and $L_{3}$ have refractive indices 1.55,1.50 and 1.20 respectively. Therefore, the arrangement corresponds to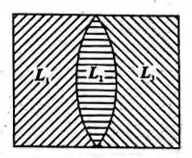
Ray Optics and Optical Instruments
Solution: