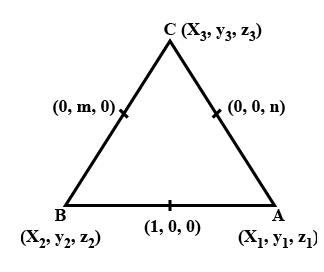
Q. In $\triangle A B C$ the mid points of the sides $A B, B C$ and $C A$ are respectively $(1,0,0),(0$, $m , 0)$ and $(0,0, n )$. Then, $\frac{A B^{2}+B C^{2}+C A^{2}}{l^{2}+m^{2}+n^{2}}$ is equal to
BITSATBITSAT 2008
Solution:
Let $A =\left( x _{1}, y _{1}, z _{1}\right),$
$B =\left( x _{2}, y _{2}, z _{2}\right),$
$C =\left( x _{3}, y _{3}, z _{3}\right)$
From the figure,
$x _{1}+ x _{2}=21, y _{1}+ y _{2}=0, z _{1}+ z _{2}=0,$ [midpoint formula]
$x _{2}+ x _{3}=0, y _{2}+ y _{3}=2 m , z _{2}+ z _{3}=0$
and $x _{1}+ x _{3}=0, y _{1}+ y _{3}=0, z _{1}+ z _{3}=2 n$
On solving, we get
$x _{1}=1, x _{2}=1, x _{3}=-1$,
$y _{1}=- m , y _{2}= m , y _{3}= m$
and $z_{1}=n, z_{2}=-n, z_{3}=n$
$\therefore $ Coordinates are $A (1,- m , n ), B (1, m ,- n )$ and $C (-1, m , n )$
$\therefore \frac{ AB ^{2}+ BC ^{2}+ CA ^{2}}{1^{2}+ m ^{2}+ n ^{2}}$
$=\frac{4 m ^{2}+4 n ^{2}+41^{2}+4 n ^{2}+\left(41^{2}+4 m ^{2}\right)}{1^{2}+ m ^{2}+ n ^{2}}$
$=8$