Q.
In an $R L C$ series circuit shown in figure, the readings of voltmeters $V_{1}$ and $V_{2}$ are $100 \,V$ and $120 \,V$, respectively. The source voltage is $130\, V$. For this situation, mark out the correct statement(s).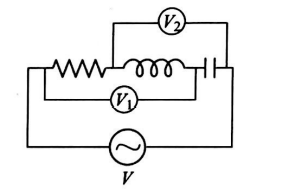
Alternating Current
Solution:
