Q.
In an LCR circuit as shown in figure, both switches are open initially. Now switch S1 is closed, S2 kept open. (q is charge on the capacitor and $\tau$ = RC is capacitive time constant). Which of the following statement is correct?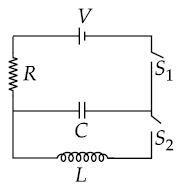
Solution:
As switch S1 is closed and switch S2 is kept open. Now, capacitor is charging through a resistor R. Charge on a capacitor at any time t is
$q=q_{0}\left(1-e^{t/\tau }\right)=CV\left(1-e^{-t/\tau }\right)$
$\left[As\,q_{0}=CV\right]$
At t $=\frac{\tau }{2},\,q=CV\left(1-e^{-\tau 2/\tau }\right)=CV\left(1-e^{-1/2}\right)$
At t $=\tau , \,q=CV\left(1-e^{-\tau/\tau}\right)=CV=\left(1-e^{-1}\right)$
At t $=2\tau,\,q=CV\left(1-e^{-2\tau/\tau}\right)=CV\left(1-e^{-2}\right)$
